Die Position des Sarkophages in der Königskammer der Cheops Pyramide - Teil 1
Die vorhandenen Höhenabweichungen in der nicht ebenen Oberfläche weisen vermutlich eine gewollte harmonische Struktur auf.

Bild 1: Sarkophag in der Cheops-Pyramide / Quelle: Internet
Präzisionsmessungen an der gut erhaltenen westlichen Außenseite ergaben folgende Ergebnisse, die von Sir W. F. Petrie im Jahr 1880 durchgeführt wurden.

Die Tabelle (Bild 2) zeigt Messergebnisse in Zoll, die mit 100 multipliziert wurden. Alle Werte wurden um den negativsten Wert angehoben, um auf Null gesetzt zu werden. Dies entspricht dem Nullsetzen einer Küchenwaage mit Tara.
Zum Beispiel entspricht der erste Wert von +10 0,1 Zoll (1 Zoll = 2,54 cm oder 25,4 mm // 0,1 Zoll = 2,54 mm).
Es ist wichtig, klare und präzise Angaben zum Startpunkt der Messung zu machen, um genaue Ergebnisse zu erzielen. Um die Abweichungen in der Oberflächenhöhe zu ermitteln, ist es wichtig, von einer praktischen Stelle auszugehen.
Eine Möglichkeit wäre, die westliche Innen- und Außenseite gleichzeitig zu vermessen, bezogen auf die Wandstärke.
Die vorhandenen Messdaten sollten in eine Tabelle eingetragen werden, um eine mögliche Struktur erkennen zu können. Beide Möglichkeiten der Messwertermittlung eignen sich zur Erkennung von Strukturen. Um eine sinnvolle Darstellung zu erhalten, müssen alle Werte um den gleichen Betrag angehoben werden. Durch das Hinzufügen von 16 zu allen Werten in der Tabelle wird erreicht, dass sich alle Messwerte auf die Nulllinie beziehen, ohne dass sich die einzelnen Beträge der Messwerte ändern.
Der Wert -16 wird zu Null und der Wert +31 wird zu +47. Die Spannweite der Min/Max-Werte bleibt bei 48, da -16 bis +31 und 0 bis +47 denselben Hub aufweisen.
Schritt 1: Alle Werte werden um 16 angehoben, um Schritt 1 abzuschließen.
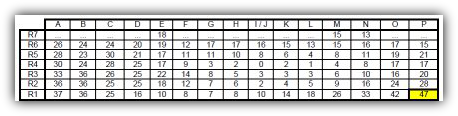
In Tabelle 1, die eine Höhentabelle ohne negative Werte darstellt, fällt auf, dass Werte für Spalte I bzw. J fehlen. Es wird vermutet, dass entweder ein Übertragungsfehler aus den ursprünglichen Aufzeichnungen vorliegt oder absichtlich 'unlogische' Werte verworfen wurden. Die Tatsache, dass es in englischen Tabellen nur eine Spalte für I und J (I/J) gibt, ist jedoch am wahrscheinlichsten.
Der größte Wert in der Tabelle beträgt 47, was zu einer maximalen Höhenabweichung von 11,938 mm führt.
Schritt 2: Darstellung
Es werden verschiedene Darstellungsarten verwendet, um mögliche Informationen in einer beabsichtigten Struktur zu erhalten. In der Reihe R7 sind Werte nicht vorhanden, die in der Darstellung nicht genutzt werden.
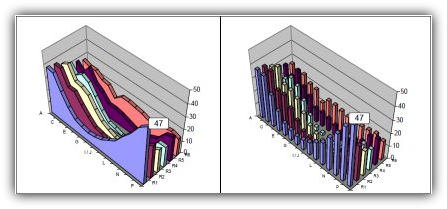
Bild 3 zeigt eine Darstellung in 3D-Flächengrafik, während Bild 4 eine Balkengrafik darstellt.
Die klare und geordnete Struktur ist unverkennbar.
Die untere Reihe (R1) weist einen großen harmonischen Verlauf auf, der nach oben hin leicht abnimmt, während die Messwerte in der Mitte am geringsten sind.
Die Gesamtstruktur erinnert an einen Trichter oder Schallgeber.
Die Messwerte werden gestapelt, um die Gesamtstruktur zu verdeutlichen.
Es handelt sich dabei um die Summe der Spalten A, B, C usw.
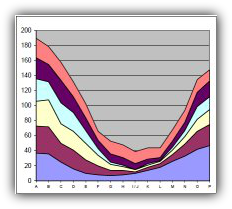
Bild 5: Gestapelte Fläche - Trend der Struktur
Schritt 3: Auswertung
Es ist eine deutliche sinusförmige Welle zu erkennen.
Eine Spalte I bzw. J und eine Spalte für die Ecken müssen hinzugefügt werden, da die Begrenzung des Sarkophags nicht vermessen wurde. Eine Spalte I bzw. J und eine Spalte für die Ecken müssen hinzugefügt werden, da die Begrenzung des Sarkophags nicht vermessen wurde. Diese dienen jedoch nur als Platzhalter und enthalten keine Werte (senkrechter schwarzer Balken ohne Wert).
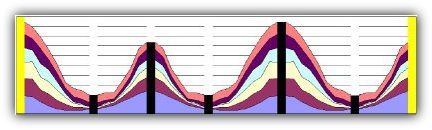
Bild 6: Einfügen von fehlenden Flächen ohne Werte (schwarze Balken)
Durch das Hinzuziehen der Ecken wird der Sinusverlauf harmonischer.
Die zusätzliche Spalte I/J sollte nicht erneut eingefügt werden, da sie nur einmal vorhanden ist und es nur einen Wert gibt. Dies unterstreicht die Qualität der Messung von Sir W.F. Henrie vor ca. 130 Jahren. Es ist zu erkennen, dass das Wellental durch das Einfügen der Spalte I/J zu breit wird. Die Qualität der graphischen Auswertung wird durch die Darstellung in Bild 3 unterstrichen.
Die Reihe R6 (obere Reihe) ist in der Mitte etwas höher als die anderen Reihen ausgeführt, was eine deutliche Richtcharakteristik zeigt. Die Abstrahlrichtung zeigt zu den Fußbodenkanten und der Einfallswinkel entspricht dem Ausfallswinkel. Mögliche Frequenzen werden von dort aus weitergeleitet und die Wellenlänge entspricht der Länge des
Sarkophags (bzw. der Innenwand = Membran). Der Sarkophag hat außen Maße von 2,276 m und innen von 1,979 m. Bei einer Temperatur von 33,33 Grad Celsius beträgt die Schallgeschwindigkeit 351,365 m/s.
Die Frequenz beträgt außen 154,378 Hz und innen 177,547 Hz bei einer Wellenlänge Lambda.
Die Wellenberge treten an den beiden Seitenkanten des Sarkophags auf und können in der Breite halbiert werden (Mittelwert). Somit ergibt sich eine mittlere Frequenz von 165,9625 Hz, oder genau 166 Hz.
Bei meiner Untersuchung des Sarkophags konnte ich eindeutige Spuren einer Bearbeitung des Bruchverlaufs feststellen.
Schritt 4: Übertragung
Im vierten Schritt, der Übertragung, ist erkennbar, dass die Form einem Trichter oder Schallgeber ähnelt. Technisch gesehen wird bei Signalquellen wie Radargeräten in eine Richtung gesendet und in der anderen empfangen.
Die Einspeisung und Auskopplung eines Signals erfolgt über einen Stiftkoppler.
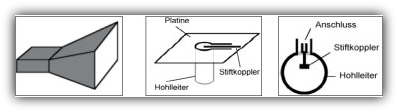
In Bild 7 sind Hornstrahler zu sehen, während Bild 8 die Einspeisung von einer Fläche oder direkt in einen Hohlleiter zeigt.
Schritt 5: Ergebnis
Die Messungen aus dem Jahr 1880 wurden als Rohdaten verwendet.
Die grafische Darstellung zeigt eine Richtcharakteristik zum Fußboden hin und erinnert an einen Trichter oder Schallgeber.
Die ermittelte Frequenz beträgt 166 Hz.
Schritt 6: Konsequenz
Eine Signaleinspeisung durch einen Stiftkoppler in den Sarkophag ist von hier aus nicht erkennbar. Daher kann die Resonanzfrequenz genutzt werden. Resonanzfrequenzen treten beispielsweise in Bauwerken auf und können sehr gefährlich sein. Seitliche Winde können Hängebrücken zerstören. Soldaten müssen den Gleichschritt beenden, da Brücken sich ansonsten aufschaukeln können. Winde an hohen Gebäuden verursachen gefährliche Schwankungen oder störende Geräusche.
Elefanten, Giraffen und Blauwale machen sich über sehr tiefe Frequenzen bemerkbar. Infraschall ermöglicht sehr hohe Reichweiten, besonders im Medium Wasser. U-Boote nutzen diese physikalischen Gegebenheiten und setzen dafür extra lange Antennen (Schleppantennen) ein.
Die Resonanzen in der Königskammer geben die Schwingungen nach oben weiter und bringen die kaskadenförmig angebrachte Struktur von unten zum Schwingen.
Dies erklärt auch den Bruch einer Platte oberhalb der Königskammer durch Resonanz. Es handelte sich höchstwahrscheinlich um einen Betriebsunfall. Eine spätere Reparatur wäre schwierig bis unmöglich.
Die Funktion als Resonanzverstärker ist leider nicht mehr gegeben aufgrund des Bruchs der Platte.
(Bitte beachten Sie das Copyright des Autors)