Die Substruktur der Nord Pyramide (manchmal auch Rote Pyramide genannt) besteht nur aus 2 unterschiedlichen Abschnitten.

 

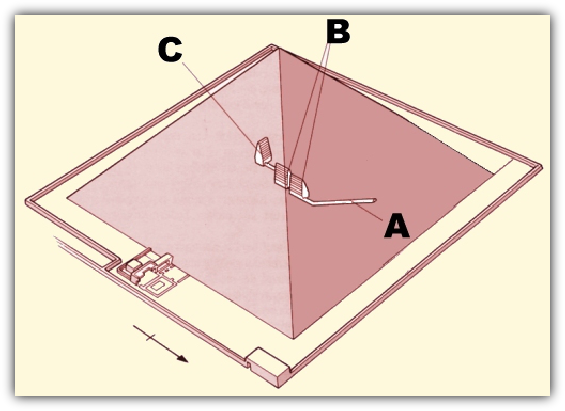
Bild 1: Die Nord- oder Rote Pyramide mit den Bezeichnungen der inneren Substruktur

 

 

Die Pyramide ist 220 m breit und 105 m hoch. Eine akustische Wellenlänge (Basismaß) von 220 m entspricht bei einer Temperatur von ca. 30° C genau 1,6 Hz. Nun werde ich versuchen, die Frequenz zu ermitteln, die in der Pyramide erzeugt wird. Diese Frequenz muss genau einem Teiler von 1,6 Hz entsprechen, ansonsten kann keine Resonanz eingekoppelt werden. Als mögliche Frequenz kommen daher nur 0,8 Hz oder 0,53 Hz in Betracht.

 

Die Maße der Grabkammer in Königsellen (KE) ergibt für 4,18 m genau 8 KE (4,19 m) und für 8,55 m genau 16 1/3 KE (8,55 m). Für die Höhe von 14,67 m ergibt sich ein Maß von 28 KE (14,66 m).

 

Das Maß der Vorkammer für 3,65 m ergibt 7 KE (3,67 m) und für 8,36 m genau 16 KE (8,38 m). Für die Höhe von 12,31 m ergibt sich ein Maß von 23,5 KE (12,30 m).

 

Für den Eingang von 62,63 m ergibt sich ein Maß von 120 KE (62,83 m). Die Breite des akustischen Kanals von 0,91 m mit einer Höhe von 1,23 stellt wieder etwas Besonderes dar. Schall kann nur winklig geführt werden. Runde Rohe verbrauchen den Schall, da interne Reflexionen den Schall dämpfen würden. Nun muss für eine eckige Schallführung der äquivalente Durchmesser ausgerechnet werden. Die Höhe des Kanals von 1,23 m ergibt in Königsellen ein Maß von 2,33 KE (1,219988 m). Für eine Breite von 0,91 m gilt ein Maß von 1,77 KE (0,926772 m).

 

Nun multiplizieren wir die Breite mal der Höhe und erhalten für die Fläche einen Wert von 1,1306507 m². Dieser Wert geteilt durch Pi ergibt 0,359897. Nun noch die Wurzel aus diesem Wert, das ergibt exakt 0,60 m als äquivalenten Radius.

 

Für eine Vorkammer habe ich einen umbauten Raum von 189,14079 m² errechnet. Die zuvor ermittelten Werte werden in der Tabelle zur Berechnung eingetragen.

 

 

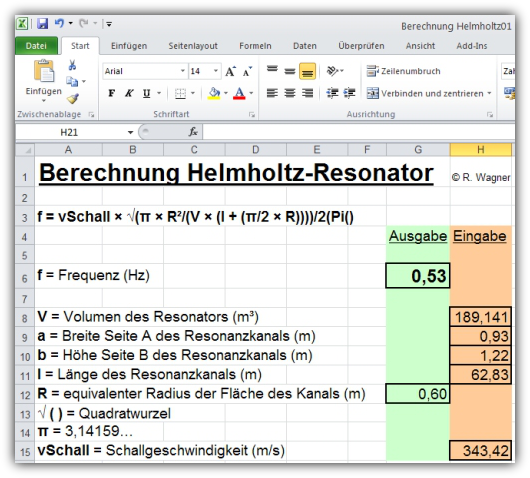
Bild 2: Berechnung der Resonanzfrequenz der Nord- oder Roten Pyramide

 

Es wird eine Resonanzfrequenz von exakt 0,53 Hz erzeugt. Das entspricht exakt einem Drittel der Wellenlänge (Basisbreite) der Pyramide von 1,6 Hz. Somit ist die Einspeisung von resonierenden Substrukturen in die gesamte Pyramide möglich.

 

Es scheint Schlüsselzahlen zu geben, wie z.B. die Maße für die Breite und Höhe des Resonanzkanals. Hier errechnet sich 0,60 m als Ergebnis (äquivalenter Radius).

 

Ich habe in der Tabellenkalkulation die Möglichkeit, verschiedene Werte einzutragen und mir das Ergebnis anzeigen zu lassen. Wenn ich hier für die Länge des Resonanzkanals nicht die Länge der aus der Roten Pyramide, sondern die Länge aus der Meidum Pyramide von 70,12 m eintrage, so erhalte ich exakt eine Frequenz von 0,50 Hz. Es scheint, als ob die Abschnitte der einzelnen Substrukturen zwischen verschiedenen Pyramiden in der Theorie austauschbar wären, da immer harmonische Ergebnisse herauskommen. Diese Schlüsselzahlen (Länge, Breite, Höhe) könnte ich in einer Tabelle für die Abmessungen im Pyramidenbau zusammenstellen.

Mit dieser Nachberechnung von austauschbaren Modulen, würde ich den Erbauern der Pyramiden mathematisch hinterher hinken ...

 

Damit überhaupt harmonische Ergebnisse herauskommen können, müssen die Angaben für die Länge, ob in Meter oder Königselle, bis zur 2. Nachkommastelle korrekt sein und auch bautechnisch umgesetzt werden.

 

 

(Bitte beachten Sie das Copyright des Autors)