Die Geige gilt als perfektes Musikinstrument. Der Geigenbau erfordert viel technisches Know-how.
Ich bin der Lösung des Rätsels um den schönen Klang der Geige ein Stück näher gekommen.
Ich habe mich mit diesem Thema wegen der Gehäuseresonanz beschäftigt. Gehäuseresonanzen gibt es sowohl in Musikinstrumenten als auch in Hallräumen.
Bevor ich die Geige technisch betrachte, möchte ich versuchen, Ihnen die Geschichte der Geige näher zu bringen. Im Internet und in der Literatur habe ich widersprüchliche Angaben über die Entwicklung des Geigenbaus gefunden. Irgendwie scheint auch hier etwas nicht zu stimmen.
In der heutigen Zeit sind wir Menschen immer darauf bedacht, die Technik weiterzuentwickeln. Das gilt besonders für den Automobilbau. Hier lösen ständig neue Modelle die alten Fahrzeuge ab. Für die im Laufe der Jahre produzierten Modelle gibt es Museen, in denen ganze Modellreihen ausgestellt sind. Nur bei den Geigen gibt es keine zeitliche Entwicklung. Die Geigen scheinen um das Jahr 1500 plötzlich aus dem Nichts aufgetaucht zu sein, jedenfalls scheint es mir so.
Die Erfindung der Geige kann keinem Erfinder zugeschrieben werden. Im Geigenbau gibt es keine Vorserien oder Modellreihen. Nicht einmal die Herkunft der Geigen ist geographisch gesichert. Oft wird behauptet, die Geigen kämen aus dem spanischen Raum. Leider gibt es dafür keine Beweise. Es wird auch behauptet, dass über Jahrhunderte versucht wurde, Geigen zu bauen. Alle gescheiterten Geigenbauversuche wurden natürlich vernichtet. Bei der Erklärung der Entstehung der Geige ist man in die gleichen Muster verfallen, wie Archäologen heute den Bau der Pyramiden erklären.
Das Fehlen einer Entwicklung im Geigenbau (vor 1500) ist für mich genauso rätselhaft wie z.B. die Existenz der Königskammer in der Cheops-Pyramide.
Woher hat man gewusst, dass es akustisch genauso zu funktionieren hat?
Stradivari begann ca. 200 Jahre später (um 1700), den Klang der Geigen zu verändern, d.h. wohlklingender zu machen. Der Klang einer Geige ist rein subjektiv und entspricht dem Geschmack der Zeit.
Wer oder was ist für den perfekten Klang einer Geige verantwortlich? Beim Pyramidenbau schließe ich das Herumprobieren mit großen und schweren Steinen für optimale akustische Verhältnisse aus.
Ich möchte die Geige aus meiner Sicht akustisch und technisch betrachten:
Die Gehäuseform der Geige ist so ziemlich das Gegenteil der Form eines rechteckigen Raumes.

Bild 1: Der Korpus einer Geige
In der Mitte der Geige befinden sich die so genannten F-Löcher. Woher der Name F-Löcher kommt, ist unbekannt. Die F-Löcher sehen eher aus wie ein normales und ein spiegelverkehrtes Fragezeichen. Denkbar ist auch eine Interpretation mit dem Summenzeichen aus der Integralrechnung. Die Abkürzung des Wortes Summe, lateinisch Summa, ist unverkennbar. Die schräge Schreibweise des Integralzeichens entspricht der amerikanischen Schreibweise. Nun möchte ich nicht spekulieren, auch wenn die Erfindung der Geige den Spaniern nach der Entdeckung Amerikas zugeschrieben wird.
In verschiedenen Forenbeiträgen habe ich versucht, die Maße normaler Geigen zu rekonstruieren. Die längste Seite des Korpus wird meist mit 35 cm bis 35,5 cm angegeben. Die obere Breite wird mit ca. 16,6 cm und die untere Breite mit ca. 21 cm angegeben. Die schmalste Seite der Geige beträgt etwas mehr als 11 cm. Die Höhe wird mit ca. 3,2 cm angegeben. Die F-Löcher haben am Anfang und am Ende sogenannte Punkte. Der Abstand zwischen den Punkten wird mit 4,4 cm angegeben. Die Länge der F-Löcher wird mit ca. 7,7 cm angegeben.
Den Geigen wird eine Resonanzfrequenz von ca. 190 Hz zugeschrieben. Diese Frequenz kann technisch nur über die F-Löcher erreicht werden. Die Funktion, eine tiefere Frequenz zu erreichen, entspricht im Prinzip den Öffnungen eines Bassreflexlautsprechers.
Nun fragen Sie sich, was mit diesem Wissen bisher erreicht wurde. Nun, lesen Sie weiter...
Eine Geige mit den Abmessungen von ca. 35 cm bis 35,5 cm hat, wenn die Zarge um 2 x ca. 3 mm abgezogen wird, eine lichte Weite des Hohlraumes von ca. 34,4 cm bis ca. 34,9 cm.
Was habe ich nun herausgefunden?
Die Länge einer Geige entspricht genau einem Tausendstel der Schallgeschwindigkeit von 343 m/s bei 20°C und 349 m/s bei 30°C. Man könnte auch sagen, dass eine Frequenz von 1000 Hz bei diesen Temperaturen einer Wellenlänge von etwa 35 cm entspricht. Man könnte auch einen neuen Begriff für diese Geige einführen. Ein passender Name wäre 1 Khz-Geige.
Betrachten wir Bild 1 und stellen uns vor, dass über die Geige eine Rasterfolie mit einer Frequenz von 1000 Hz gelegt wird. Jetzt kann man alle möglichen akustischen Frequenzen ablesen, die durch die Form der Geige bedingt sind.
Jetzt wird es noch fantastischer:
Mit meinen Berechnungen habe ich für die Königskammer in der Cheops-Pyramide eine Resonanzfrequenz von ca. 1,66 Hz errechnet. Das entspricht einer Wellenlänge der gesamten Breite der Pyramide, oder anders ausgedrückt, die Wellenlänge passt zur Breite der Cheops-Pyramide.
Welches Objekt hat eine Wellenlänge, die der Resonanzfrequenz der Geige entspricht?
Die Maße der Geige, die ich oben rekonstruiert habe, ergeben ein Volumen von ca. 1,8 Liter Luft. Für die F-Löcher erhalte ich 13 cm² bis 15 cm². Für die Tiefe des Bassreflexkanals nehme ich eine Wandstärke von ca. 3 mm an. Ich erhalte eine Eigenfrequenz der Geige von ca. 190 Hz bis 195 Hz. Das Ergebnis der berechneten Eigenfrequenz stimmt mit den Angaben in der Literatur überein.
Ohne die F-Löcher hat die Geige eine Resonanzfrequenz von ca. 1000 Hz. Mit den F-Löchern hat die Geige eine Resonanzfrequenz von ca. 195 Hz.
Für uns Menschen klingt eine Geige sehr harmonisch. Wir können uns dem Zauber des Klanges nicht entziehen. Irgendwie erreicht uns Menschen der Klang einer Geige! Rechnen wir nun die Schallgeschwindigkeit von 343 m/s durch 195 Hz. Als Ergebnis erhalten wir eine Wellenlänge von ca. 1,76 m.
Jetzt frage ich sie, wie groß sie sind. Fakt ist, dass der abgestrahlte Schall bzw. die Wellenlänge Ihren Körper zu mindestens 90 Prozent beschallt.
Empfinden wir deshalb den Klang einer Geige als harmonisch?
Die tatsächlichen Maße einer Geige stellen ein Optimum für den Menschen dar.

Bild 2: Meine berechneten Proportionen einer Geige
Schwarz (Länge der Geige): Von oben gesehen ein Drittel und drei Fünftel der Geigenlänge.
Grüne Schrift (Breite der Geige): Die obere Breite einer Geige ist etwa halb so breit wie die Länge der Geige. Die Mitte ist etwa ein Drittel so breit und die untere Breite entspricht etwa zwei Drittel der Geigenlänge. In der Summe (1/2 + 1/3 + 2/3) entsprechen die 3 Bereiche einer Breite von 1,5. Für die Geometrie der Geige ergibt sich ein Verhältnis von 1,5 : 1. Ein Zehntel der Geigenlänge entspricht ungefähr der Höhe einer Geige. Durch diese harmonischen Brüche ist ein besonders harmonisches Klangbild (Tonleiter) zu erwarten.
Diese harmonischen Brüche sind mir erst beim Betrachten einer Geige aufgefallen...
Eine weitere interessante Tatsache ist, dass die F-Löcher genau im Verhältnis des Goldenen Schnittes liegen (Wert=1,618, etwas oberhalb der Position 3/5 (Wert=1,666)), angedeutet durch die kleinen roten Striche in Bild 2. Das ist natürlich reiner Zufall, denn der Goldene Schnitt wurde erst im 19. Jahrhundert so richtig bekannt und hatte außerhalb der Mathematik keine Berechtigung. Schon um 300 vor Christus soll der griechische Mathematiker Euklid den Goldenen Schnitt angewendet haben.
Mit diesem Beitrag konnte ich etwas völlig Neues zeigen. Wichtig war mir die Betrachtung von schwingenden Wänden, sei es im Instrumentenbau oder im Pyramidenbau. Ich habe die Proportionen einer Geige ausgewertet (Bild 2) und gehe NICHT davon aus, dass Geigenbauer über ähnliche Kenntnisse verfügen. Was ich im Internet an Homepages oder technischem Hintergrundwissen über die technische Akustik einer Geige lesen konnte, stimmt mich sehr traurig... ich hatte viel mehr erwartet!!!
Im Geigenbau gibt es meiner Meinung nach ein ständiges Kopieren von Vorgängern, also eine Kopie von einer Kopie von einer Kopie von einer Kopie und so weiter.
Bei der Konstruktion eines neu zu bauenden Musikinstrumentes habe ich die wildesten Formeln und Zirkelkonstruktionen gefunden. Alles Unsinn - das Wesentliche wurde nicht erkannt. Es sind die harmonischen Proportionen oder Brüche einer Bruchrechnung.
Sollte ein Leser entsprechende Kenntnisse haben (Resonanzkörper = Harmonie durch Bruchrechnung), bitte ich um sofortige Mitteilung. Ich werde diesen Text sofort ändern. Ansonsten gehe ich weiterhin davon aus, dass es sich um einen Nachbau alter Musikinstrumente handelt, egal welcher Art.
Die Form einer Geige oder einer Gitarre ist aus der mathematischen Bruchrechnung entstanden. Die Proportionen verhalten sich musikalisch sehr harmonisch. Daraus ergeben sich optimale Formen für akustische Räume.
Um einen akustischen Hintergrund dieser optimalen Form auch in Gebäuden erkennen zu können, möchte ich Sie, liebe Leserinnen und Leser, kurz auf die Insel Malta entführen. Alle Tempel Maltas haben einen akustischen Hintergrund. Nachdem Sie die Form einer Geige in ihren Proportionen näher kennengelernt haben, betrachten Sie bitte das folgende Bild des Tempels von Tarxien unter dem Gesichtspunkt der Akustik.
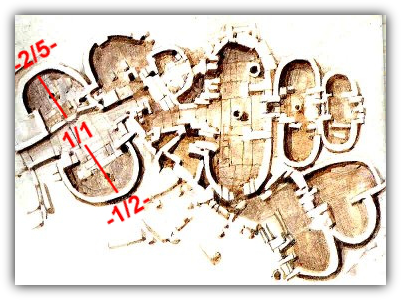
Bild 3: Der Tempelkomplex von Tarxien auf Malta. (Quelle: Museum)
Man erkennt sofort die Hallräume, die an ein Musikinstrument erinnern. Ich betrachte nun den linken Hallraum. Die obere Breite des Raumes entspricht 2/5 und die untere Breite des Raumes entspricht 1/2 der Gesamtlänge des Hallraumes. Die Länge des Hallraumes ergibt die tiefste, gerade noch hörbare Frequenz von 20 Hz bis 25 Hz.
An dieser Stelle wird natürlich ein Copyright fällig.
(Bitte beachten Sie das Copyright des Autors)