Auf dem Plateau von Gizeh in Ägypten (in der Nähe der Cheops-Pyramide) gibt es einen tiefen Schacht, der erst vor etwa 80 Jahren entdeckt wurde. Es ist der berühmte Osiris-Schacht. Das Schachtsystem reicht bis in eine Tiefe von ca. 30 m und weist die typischen Substrukturen anderer Pyramiden in Ägypten auf.
Über dieser Substruktur wurde keine Pyramide (Steinhaufen) errichtet.
Der Schacht führt senkrecht nach unten und hat 3 Ebenen, die nur mit einer entsprechenden Leiter zu erreichen sind. Hier hat niemand gewohnt, hier wurde auch niemand bestattet. Das hat mein Interesse geweckt, denn dieses Bauwerk muss eine akustische Funktion haben.
Mich interessieren die Dimensionen des Schachtes. Ich möchte die Resonanzfrequenz dieser scheinbar fertigen Konstruktion berechnen.
Wie immer ist das Maß der Königselle (KE) Pi/6 m oder 0,5236 m. Das ist das Maß für die akustische Wellenlänge in Metern.
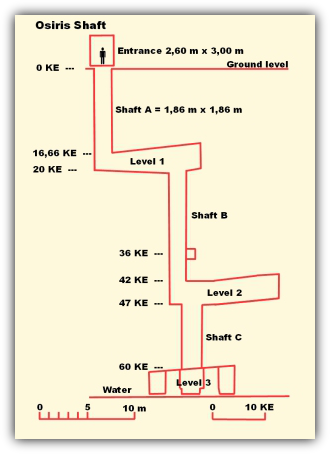
Abbildung 1: Meine Skizze des Osiris-Schachtes
In dieser Skizze habe ich die Maße in Königsellen (KE) angegeben. Eine Angabe in Metern o.ä. erscheint hier nicht immer sinnvoll.
Beginnen wir mit den Abmessungen des Eingangsbereiches des Schachtes Osiris. Der Schachteingang ist mit 2,60 m x 3,00 m angegeben. In diesen Abmessungen steckt mehr Pi als man denkt.
Ich erhalte einen harmonischen Wert von 4,96 (fast 5), wenn ich 2,60 m durch die Königselle teile. Dieser Wert ist harmonisch mit 5 KE. Für 3,00 m, geteilt durch die Königselle, erhalte ich einen unharmonischen Wert von 5,73. Dieser unharmonische Wert von 5,73 ist untypisch für Pyramidenmaße.
Eigentlich sollte ich mich jetzt einem anderen, leichteren Thema widmen, aber aufgeben ist nicht angesagt. Die Lösung des Rätsels liegt wie immer in der Akustik.
Um in der Akustik etwas konstruieren oder berechnen zu können, ist eine runde Form zu bevorzugen. Leider gibt es auf dem Gizeh-Plateau keine runden Formen, wie z.B. Rohre, kreisrunde Räume etc. Es wurde immer eckig geplant und gebaut. Das ist nicht weiter tragisch, man muss nur für eine Berechnung in runde Formen umrechnen.
Jetzt rechnen wir einfach die Fläche von 2,60 m x 3,00 m aus, das sind 7,8 m². Nun suchen wir den Radius für eine Kreisfläche von ebenfalls 7,8 m². Dafür gibt es die bekannte Formel A = r² x Pi. Um den äquivalenten Radius zu erhalten, stellen wir die Formel um und dividieren 7,8 m² / Pi. Aus dem Ergebnis ziehen wir die Wurzel und erhalten für den Radius den Wert r = 1,57 m.
Fazit:
Eine rechteckige Fläche von 2,60 m x 3,00 m entspricht einer kreisförmigen Fläche mit einem Radius von 1,57 m.
Ups... 1,57 m entspricht 3 x 0,5236 m oder drei Königsellen (3 KE).
Also ist der äquivalente Durchmesser der Eingangsfläche (2 x Radius) 6 KE.
6 KE in Metern sind genau 3,14 m, also Pi in m.
Für jedermann sichtbar existiert Pi auf dem Plateau von Gizeh.
Niemand vor mir hat es geschafft, Pi auf dem Gizeh-Plateau zu beweisen, und das auf so einfache Weise!
Ein Wert von 3,14 oder Pi wurde auf dem Gizeh-Plateau für unmöglich gehalten und immer bestritten.
----------
Betrachten wir nun den Durchmesser des Schachtes. Der Durchmesser beträgt 1,86 m. Schon wieder so ein untypisches Maß - weit gefehlt. Der Schacht ist quadratisch. Die Flächenberechnung ergibt 3,4596 m². Nun teilen wir diesen Wert durch Pi und ziehen die Wurzel aus dem Ergebnis. Für den Radius erhalten wir den Wert r = 1,049 m.
2 Königsellen entsprechen 1,047 m. Die Abweichung von 2 mm geht in der Messunsicherheit unter. Der äquivalente Durchmesser des Schachtes entspricht 4 KE (2,094 m) oder 2/3 Pi. Die Tiefe des Schachtes beträgt 20 KE (10,47 m). Bis zum Eingang der Kammer habe ich eine Tiefe von 16,66 KE (8,73 m) ermittelt.
Bis zu dieser Stelle ist der Schacht ca. 10 m tief. Das entspricht in etwa den Abmessungen eines Aufzugsschachtes. Wie gesagt, ca. 10 m tief. Diese Größenordnung (4 Stockwerke) musste ich Ihnen noch einmal zeigen.
Vom vertikalen Schacht geht es horizontal in die Kammer 1 (Ebene 1). Die Einstiegshöhe beträgt 3,33 KE (1,75 m).
Das Volumen der Kammer 1 ergibt zusammen mit der Schachttiefe und dem Schachtdurchmesser eine ganz bestimmte Resonanzfrequenz.
Die Wände sind nicht parallel. Das mittlere (angenäherte) Volumen der Kammer 1 beträgt ca. 90,4 m³. Die Schachttiefe wird mit 16,66 KE (8,73 m) angesetzt.

Tabelle 1: Resonanzfrequenz im Osiris-Schacht.
Das Ergebnis der Resonanzfrequenz ist 3,33 Hz. Ich hatte einen Wert von ca. 3,14 Hz vermutet, da im Osiris-Schacht überwiegend der Wert von Pi vorliegt.
----------
Die Kammer 2 dient nur zur akustischen Verstärkung und hat das bekannte Aussehen von kammartigen Lagerkammern.
Die Frequenz wird in Kammer 3 erzeugt, also nach genau 60 KE (31,41 m bzw. 10 Pi). Sehr interessant ist das Wasser, das auf der Sohle des Osiris-Schachtes gefunden wurde. Die Herkunft des Wassers ist unbekannt, eine Quelle scheidet aus. Das Wasservorkommen ist künstlich angelegt. Die Bedeutung des Wasservorkommens ist völlig unklar, eine Funktion scheint nicht vorhanden zu sein. Die Fachwelt steht wieder vor einem Rätsel.
Aus akustischer Sicht macht eine glatte Wasseroberfläche Sinn. Sie kann als Indikator für eine Resonanzfrequenz dienen. Bei Resonanz bilden sich geometrische Formen auf der Wasseroberfläche.
Wenn Sie mehr über diese geometrischen Formen erfahren möchten, dann googlen Sie im Internet nach - Chladnische Klangfiguren. Lassen Sie sich die entsprechenden Bilder anzeigen und achten Sie besonders auf die Dreiecksformen. Sie kommen der Klangfigur einer Pyramide sehr nahe. (Die Erzeugung dieser Figuren ist ein sehr interessantes Thema, das mir einige meiner Leser als ihr Hobby mitgeteilt haben).
In den Substrukturen der Pyramiden wurde gelegentlich Quecksilber gefunden. Man spricht sogar von kleinen Seen. Anstelle von Wasser könnte Quecksilber in früheren Zeiten als Indikator gedient haben. Dabei ist zu beachten, dass Quecksilber mehr als 13-mal schwerer ist als Wasser und andere sichtbare Resonanzen erzeugt.
Quecksilber gilt heute als gesundheitsschädlich. Für mich gilt - alles übertrieben... Eventuelle Dämpfe (z.B. Metallgeruch) sollen nur in kleinen, unbelüfteten Räumen und bei hoher Konzentration schädlich sein. Unter normalen Umweltbedingungen wird Quecksilber nicht eingeatmet. Auch das Verschlucken von Quecksilber gilt als schädlich - wer tut das schon? Wie sehr Quecksilber heute als gefährlicher Stoff verteufelt wird, sieht man daran, dass quecksilberhaltige Materialien (z.B. Amalgam, Thermometer etc.) verboten sind. So gefährlich kann Quecksilber gar nicht sein, denn ohne Quecksilber hätte es die Pharmaindustrie schwer. Vor etwa 100 Jahren wurde empfohlen, bei Verstopfung geringe Mengen Quecksilber einzunehmen.
(Bitte beachten Sie das Copyright des Autors)