Die Pyramide hat in der allgemeinen Literatur die offiziellen Maße 121 m x 109 m. Die Höhe wird mit 60 m angegeben. 109 m ist aber kein harmonisches Maß. Hier wurde wohl falsch gemessen. Mit GoogleEarth lässt sich das schnell überprüfen.

Abbildung 1: Grundriss der Pyramide von Djoser mit GoogleEarth
Die Abmessungen wurden mit ca. 120,5 m auf der einen Seite und 105 m auf der anderen Seite gemessen. Nun rechnen wir diese Werte in Königsellen um. Für 120,5 erhalten wir 230 Königsellen, genau 120,428 m. Dieser Wert von 230 KE ist ein harmonisches und oft verwendetes Maß für die Breite von Pyramiden. Auch 105 m ergibt ein harmonisches Maß von 200 Königsellen, also genau 104,72 m.
Die gleichen ungeprüften Werte wurden über die Jahrhunderte immer wieder reproduziert.
Die Grundrissmaße der Pyramide von Djoser ergeben 200 KE x 230 KE für die Seitenlänge.

Bild 2: Seitenansicht der Stufenpyramide, (Bild lizenzfrei)
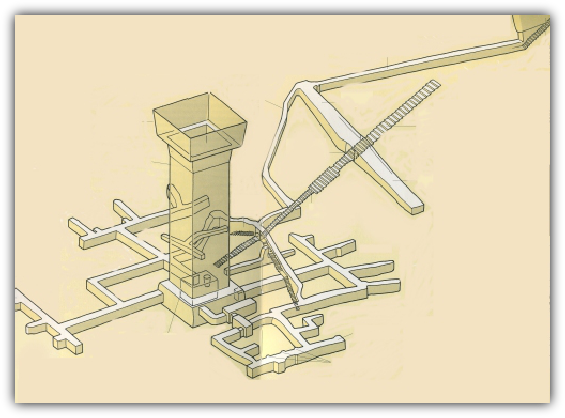
Abbildung 3: Die Unterkonstruktion mit dem 28 m tiefen und 7 m x 7 m breiten Schacht.
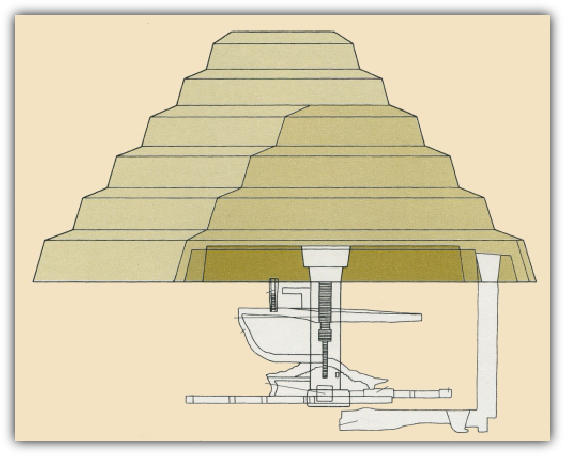
Abbildung 4: Lage und Anordnung des Schachtes unter der Pyramide
Es sieht aus, als ob eine riesige Orgelpfeife an der Pyramide befestigt wäre. In Abbildung 3 ist die Länge des Schachtes mit 28 m angegeben, mit einer quadratischen Fläche von 7 m x 7 m.
Schaut man sich Abbildung 4 an und überträgt die Abmessungen der Unterkonstruktion auf Bild 2, so werden erst jetzt die gewaltigen Dimensionen im unterirdischen Bereich deutlich.
Um hier eine sehr tiefe Frequenz dieser Konstruktion zu berechnen, muss zunächst eine Schwingfrequenz der Pyramide berechnet werden. Bei einer Abmessung von 200 KE ergibt sich eine Frequenz von 3,333333 Hz, bei 230 KE eine Frequenz von 2,8956 Hz. Der Mittelwert der beiden Frequenzen beträgt etwa 3,14 Hz.
Die Höhe des Schachtes, oder wie hier die Länge einer Orgelpfeife, beträgt 28 m. Der Schacht hat oben einen so genannten Wulst. Akustisch muss dieser Wulst von der Länge abgezogen werden. Geschätzte 3 m ergeben dann eine akustische Gesamtlänge von ca. 25 m.
Ich nehme an, wie bei allen anderen Pyramiden auch, dass der Schacht eine Gesamtlänge von ca. 25 m hat. Zur Berechnung der Lambda-Viertels muss nun durch 4 geteilt werden. Da es sich hier um eine einseitig geschlossene Röhre handelt, muss der Wert nochmals durch 2 geteilt werden, also insgesamt durch 8. Der Wert von Pi x m multipliziert mit 8 ergibt 25,13 m.
Akustisch kann in diesem Rohr nur eine Resonanzfrequenz von ca. 3,14 Hz auftreten.
Die Eigenfrequenz des Schachtes von 3,14 Hz entspricht genau der Eigenfrequenz der Pyramidebreite von ebenfalls 3,14 Hz.
Mich persönlich fasziniert diese gigantische unterirdische Substruktur. Wer hat sie erdacht, technisch geplant und realisiert?
(Bitte Copyright des Autors beachten)