Die Entschlüsselung des Neigungswinkels der Roten Pyramide wird hier detailliert erklärt.
Im Gegensatz zu den zuvor behandelten drei Pyramiden auf dem Gizeh-Plateau gibt es hier eine andere Rechenregel. Der Neigungswinkel kann bei der Roten Pyramide nicht nach der vorherigen Methode berechnet werden.

Bild 1: Die Rote Pyramide in Dahschur, oder auch Nord Pyramide genannt
Die Rote Pyramide in Dahschur, auch bekannt als Nordpyramide, ist die dritthöchste und vom Volumen her die drittgrößte Pyramide in Ägypten.
Mit einer Basis von 220 m, einer ursprünglichen Höhe von 109,5 m und einer heutigen Höhe von 104 m hat sie den kleinsten Neigungswinkel aller Pyramiden und ist die flachste.
Die Neigung beträgt 43° 22'.
Die Informationen auf Wikipedia sind korrekt. Der angegebene Winkel von 43° 22' entspricht einem Dezimalgrad von 43,3666666°.
Der Neigungswinkel wurde berechnet, indem die ursprüngliche Höhe durch das halbe Basismaß geteilt und dann die Arkustangensfunktion angewendet wurde. Das Ergebnis ist ein Neigungswinkel von 44,869486°.
Die heutige Höhe geteilt durch das halbe Basismaß ergibt 0,945454. Daraus ergibt sich ein Neigungswinkel (arctan) von 43,393980 Grad.
Beide Werte (44,869486°, 43,393980°) weichen von der Angabe von 43,3666° ab.
Die Angabe des Neigungswinkels aus der obigen Tabelle in Wikipedia© ist falsch.
Für die heutige Höhe von 104 m werden 200 Königsellen eingesetzt (Abweichung: 0,72 m). Die Basisbreite von 220 m entspricht 420 Königsellen (Abweichung: 0,09 m).
Die wichtigen Parameter der Roten Pyramide sind wie folgt:
Seite a (Grundseite) = 420
Höhe h = 200
Höhe ha = 290
Seitenkante s = 358,05
Diagonale d = 593,97
Umfang u = 1680
Grundfläche G = 176400
Mantelfläche M = 243600
Oberfläche O = 420000
Volumen V = 11760000
Neigung der Seitenflächen = 43,603°
Neigung Seitenkante = 33,958°
Seitenfläche AS = 60900
Die flachste Pyramide in der diagonalen Ansicht, welche die breiteste Ansicht dieser Pyramide darstellt, ist ausschlaggebend. Das Geheimnis liegt in der Breite.
Es wird der Winkel der Seitenkante verwendet, nicht der Winkel der Seitenfläche. Der Gegenwinkel zur Seitenkante beträgt 56°. Folglich beträgt der gesamte Breitenwinkel an der Spitze der Pyramide 112° (2 x 56°).
Das sogenannte Pyramidion fehlt oben auf der Pyramide. Es ist nicht mehr eindeutig zurückrechenbar. Dadurch verändert sich der Winkel an der Spitze grob um etwa 0,5° auf 34,5°. Für den gesamten Breitenwinkel an der Spitze der Pyramide sind exakt 111° anzusetzen.
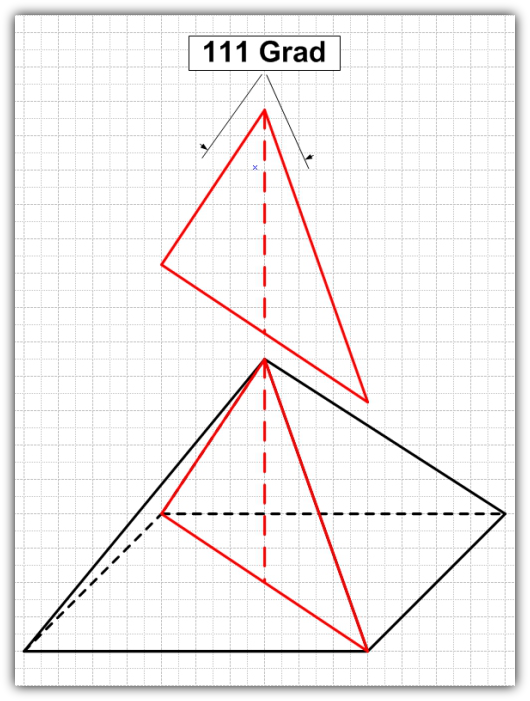
Bild 2: Der harmonische Pyramidenwinkel an der Spitze beträgt 111 Grad.
Der Neigungswinkel der Roten Pyramide ergibt sich aus der Silhouette der gesamten Pyramidenbreite, die ebenfalls einen Winkel von 111 Grad aufweist.
(Bitte beachten Sie das Copyright des Autors)