Ein akustischer Resonator (nach Hermann Helmholtz) erzeugt eine Resonanzfrequenz. Ein solcher Resonator ist z. B. als Flasche bekannt, die einen tiefen Ton erzeugen kann, wenn man seitlich am Flaschenhals entlang bläst. Das Prinzip des Resonators ist nicht auf eine Flasche beschränkt. Auch Musikinstrumente, Muscheln oder große Hallräume funktionieren nach diesem physikalischen Prinzip. Die Formel lautet:
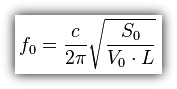
Abbildung 1: Formel für die Resonanzfrequenz, Quelle: Wikipedia
Ein einfaches Beispiel für die Resonanzfrequenz einer Weinflasche:
Nach obiger Formel hat eine 1-Liter-Weinflasche mit einer Halslänge von ca. 7 cm und einem Innendurchmesser des Flaschenhalses von ca. 2,1 cm, bei seitlichem Anblasen, eine Resonanzfrequenz von ca. 110 Hz.
Für Höhe, Breite und Tiefe werden 10 cm eingegeben, was ein Volumen von 1 Liter ergibt. Für die Länge des Flaschenhalses werden 7 cm und für den Durchmesser 2,1 cm eingegeben.
Die Resonanzfrequenz der Königskammer:
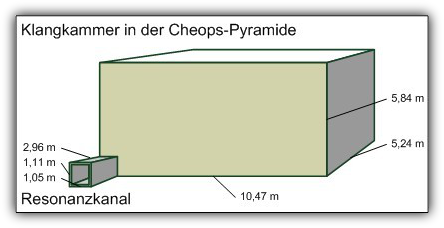
Abbildung 2: Beispielwerte aus der Dimensionierung der Königskammer
Die Berechnung (nach obiger Formel) der Resonanzfrequenz mit den Abmessungen der Königskammer ergibt eine tiefe Resonanzfrequenz von 1,66 Hz.
In Kombination mit den vorgeschalteten Fallsteinen vor der Königskammer ergibt sich eine Länge des Resonanzkanals von ca. 385 cm, was genau 1,5 Hz entspricht.
Die zugehörige Wellenlänge von 1,5 Hz entspricht der Pyramidenbreite der Cheops-Pyramide von 230 m.
Flächenberechnung von eckig nach rund:
Alle Gangsysteme in Pyramiden sind rechteckig. Um eine Berechnung nach obiger Formel durchführen zu können, benötigen wir den Durchmesser einer gleich großen Fläche eines entsprechenden Kreises.
Eine rechteckige Fläche mit den Abmessungen 111 cm x 105 cm ergibt 11655 cm², also A = 11655 cm².
Die Formel zur Berechnung eines Kreises lautet: A = Pi x r². Dividiert man nun die Fläche durch den Wert von Pi, so erhält man r², also 11655 / Pi und erhält 3709,9 cm². Um den Wert von r zu erhalten, ziehen wir die Wurzel aus 3709,9 cm² und erhalten 60,91 cm für den Radius. Für den äquivalenten Durchmesser nehmen wir 60,91 cm x 2 und erhalten 121,8 cm für den gesuchten Durchmesser einer entsprechenden Kreisfläche.
Beispiel einer Formel zur Mündungskorrektur:

Abbildung 3: Formel der Resonanzfrequenz für die korrigierte Länge eines beidseitig offenes Rohres, Quelle: Wikipedia
(Bitte beachten Sie das Copyright des Autors)