Anhand eines Beispiels berechnen wir die Sektoren einer Sonnenuhr. Hier bietet sich die kleine Anlage Torre Llafuda an. Hier fühlt man sich wie in eine Märchenwelt zurückversetzt. Diese Steinsetzung ist flach gehalten und gut überschaubar.

Bild 1: Torre Llafuda
Für die nachvollziehbare Auswertung verwende ich nur Bild 1. Die gemessenen Werte sind in Bildpixel aus Bild 1 entnommen. Meine Werte lassen sich leicht überprüfen.

Bild 2: Torre Llafuda mit den interessanten Stellen in der Auswertung
Die Strecke 1-2 und die Strecke 3-4 ergeben je 22 Bildpixel. Die Strecke 2-3 ergibt 88 Bildpixel. Als Teilung ergibt sich 22 | 88 | 22, oder auch 1 | 4 | 1. Der Sektorstein hat also insgesamt 6 Teilungen. Für die Höhe der Speiche sind 105 Bildpixel ausgemessen. Die Vermessung ist damit erst einmal abgeschlossen.
Für die Breite des Sektorsteins ergibt sich ein Maß in der Summe von 132 Bildpixel. Für die Höhe der Speiche als Radius mit 105 Bildpixel lässt sich ein Umfang von 660 Bildpixel (U = 2 x r x Pi) ausrechnen. Wir teilen 660 Bildpixel durch die Breite des Sektorsteins von 132 Bildpixel und erhalten die Zahl 5. Also wird der Verlauf der Sonne in 5 Sektoren unterteilt. Jeder Sektorstein hat 6 Teilungen. Es ergibt sich eine Gesamtteilung von 30 Einheiten. Ein Tag hat heute 1440 Minuten. Wir teilen nun 1440 Minuten durch 30 Sektoren und erhalten für die kleinste Zeiteinheit (Teilung) dieser Sektoruhr exakt 48 Minuten.
Ich hatte nur vereinzelt die Möglichkeit, vor Ort den Schattenwurf von Sektoruhren zu überprüfen. Nun habe ich mit Hilfe von Computersoftware eine weitere Überprüfung vorgenommen und Längenabmessungen, Kalenderzeiten, Sonnenstände, Koordinaten, usw. zur Berechnung eingegeben.
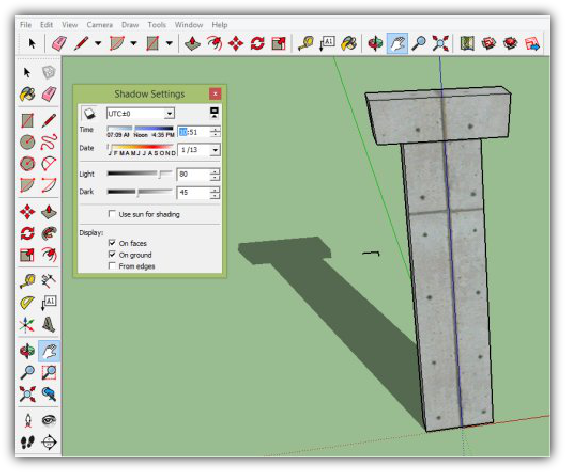
Bild 3: Auswertung in 3D mit CAD Software - hier: Torre de Galmes
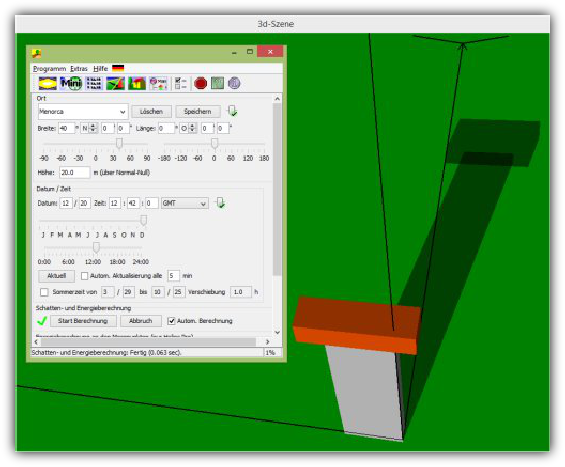
Bild 4: 3D-Software zur Berechnung des Schattenwurfs für Sonnenkollektoren.
Die Konstruktion einer Sektoruhr wird in Bild 4 dargestellt. Die Abmessungen sind:
Speiche - Höhe: 3,14 m, Breite: 99 cm; Sektorstein - Überhang rechts und links: 33 cm, Breite: 1,65 m (33 + 99 + 33) mit den Teilungen 1 | 3 | 1.
Für den Umfang gilt ein Maß von 19,74 m, das durch die Sektorbreite von 1,65 m geteilt wird. Das Ergebnis ergibt 12 Stunden. Jeder Sektorstein hat 5 Teilungen. Der tägliche Sonnenlauf wird in 60 Teilungen unterteilt. Für unsere täglichen 1440 Minuten ergibt sich für die kleinste Teilung eine Zeit von 24 Minuten.
Am 21.06. benötigt man für die Strecke 3-4 24 Minuten und für die Strecke 1-4 120 Minuten. Auch gibt es andere glatte Teiler beim Schattenlauf am Boden. Zum Beispiel benötigt man am 21.12. 12 Minuten für die Strecke 3-4 und 60 Minuten für die Breite des Sektorsteins (Strecke 1-4).
Zusammenfassend ergibt sich aus der Auswertung des Schattenwurfs am Boden ein Abbild der in Stein berechneten Teilungen. Damit ist bewiesen, dass die Erbauer dieser Anlagen die Mathematik in Stein verewigt haben und die Konstruktion von Teilungen in Sektoren nicht dem Zufall zugeschrieben werden kann.
Die Erbauer dieser Anlagen haben hier die Mathematik in Stein verewigt...
(Bitte beachten Sie das Copyright des Autors)